[作成中]電流の問題(電力・発熱)の学習法

 

電流の強さ

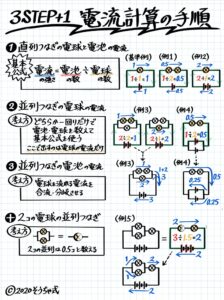
まず、いくつかの電球が配置された直列回路と並列回路での各所の電流の強さを計算できるようにする

電流計算の基本

説明書き

この後の電力・発熱で重要になるので憶えておきたいのは

➀直列回路では電流の大きさは等しく、並列回路では合流・分岐させると等しい

 

②並列回路での電流の大きさは、電球の数と反比例(逆比)になっている

 

ことです。

抵抗の大きさ

抵抗の大きさ

電球も抵抗の一種。光を発するところ(フィラメント)が抵抗になっている。

電球2個がつながったものBは電球1個Aに比べると抵抗が2倍になる。3個つながったものCは3倍になる

((1:2の抵抗値＝1：2の電球 の図))

抵抗の比

抵抗の大きさは本来は「Ω(オーム)」という記号で表されるが、ここでは他の抵抗の大きさとの「比」で表す

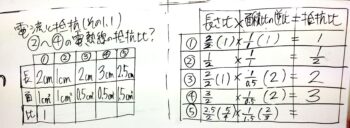
抵抗の大きさは「抵抗の断面積」と「抵抗の長さ」で決まる

長さには比例

長くなればなるほど抵抗は大きくなる。

長さが1:2の抵抗AとBの抵抗の大きさの比は1:2になる。

断面積には反比例(逆比)

断面積が大きく(太く)なればなるほど抵抗は小さくなる。

長さが1:2の抵抗AとBの抵抗の大きさの比は2:1(または11:12)になる。

表を使った練習問題

((電池の無い直列回路図を追加))

合成抵抗

直列にならんだ抵抗は抵抗比を合計すると一つの抵抗に合成できます。

これを使うと直列と並列を合成した問題が解けます。

(図)

抵抗の比が出せるようになれば電力発熱の基礎は終了です

抵抗比と電力

電力

「電力=電流×電圧」で計算できるが、中学受験では「電圧」を扱わないので「電力=電流×電流×抵抗」で考える。

重要なのは、直列/並列での比例/反比例を「憶える」こと。

「電力=電流×電流×抵抗」なので電流を2倍すると電力は4倍になる。これも憶えておくこと

直列回路

抵抗比1:2の抵抗Aと抵抗Bを直列につなぐと、回路全体に流れる電流は等しい(➀とする)ので、「電力=電流×電流×抵抗」より、Aで発生する電力は➀×➀×1、Bでは➀×➀×2になる。

つまり抵抗1:2のAとBは電力比も1:2になっている。

すなわち、直列回路では電力比は抵抗比と比例する

並列回路

 

つまり抵抗1:2のAとBの電力比は2:1になっている。

すなわち、並列回路では電力比は抵抗比と反比例する(逆比)

小まとめ

	直列つなぎ	並列つなぎ
抵抗比1:2の抵抗AとBに発生する電力	比例(1:2)	反比例(2:1)
発生する熱量	比例(1:2)	反比例(2:1)
水の上昇温度 (例)15°の水を加熱	比例(1:2) (例)A:15→20°、B:15→25°	反比例(2:1) (例)A:15→25°、B:15→15°

直列と並列の組み合わせ

並直列回路

図のような回路で各抵抗での電力比を出してみます。

(())

直列部分は合成して一つの抵抗にします

(())

2つの抵抗が並列になっているので、逆比で電力比を出します。

(())

合成抵抗を元に戻して、比を更に分けます。

(())

分数混じりですが、電力の比が出ました。

直並列回路(基本)

このような回路での電力比を求めます

((図))

同じ比の抵抗が並列につながっている場合は、電球の場合と同じで1/2の大きさになります

((電球))

したがって、1/2の比の抵抗に合成できます。

この比を使って、直列になっているもう一つの抵抗との比が分かります(整数にしておく)

((図))

直並列回路(応用)

ここから先は

並列で分岐する時、電流は抵抗に反比例

電力=電流×電流×抵抗」

2つを使う応用問題です。

 

抵抗と発熱

抵抗比と発熱

発熱量は電流に比例するので、上で見た関係がそのまま成り立つ

 

水温上昇の問題

抵抗比との関係

水温の上昇温度(ただの温度ではない)は発熱量に比例するので、ここでも同じ関係が成り立つ

つまり、直列では比例して並列では反比例(逆比)する

他の要素

実際の問題では「加熱時間」と「水の量」が異なることもある。

加熱時間が長いほど水温の上昇温度も大きくなる(比例)

水の量が多いほど水温の上昇温度は小さくなる(反比例,逆比)

 

練習問題

 

 

電球と電力

ワット

ワットは電力の単位で「電力=電流×電圧」

(ここからは流し読み)

電球に記されているワット数は、ある電圧に並列につないだ時(電圧が等しいので)に流れる電流を表している。

例えば「100V60W」という電球は100Vの電源につないだ時に60Wの電力(つまり0.6Aの電流が流れる)ことを意味する。

(ここまで流し読み)

ワット数と電球の明るさ

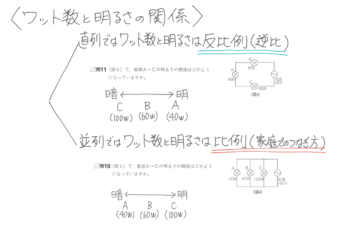
直列と並列

大切な事は、家庭のコンセントに繋いだ時(並列つなぎになる)ワット数が大きくなると流れる電流は増えるつまり明るくなるということ。

	直列つなぎ	並列つなぎ (家庭のコンセント)
ワット数と 明るさの関係	反比例 (ワット数が大きければ 暗くなる)	比例 (ワット数が大きければ 明るくなる)

これは、抵抗比と電力発熱の関係とは逆になっているので注意

	直列つなぎ	並列つなぎ
抵抗比と 電力発熱の関係	比例 (抵抗比が大 →電力発熱も大)	反比例 (抵抗比が大 →電力発熱は小)
ワット数と 明るさの関係	反比例 (ワット数が大 →暗くなる)	比例 (ワット数が大 →明るくなる)

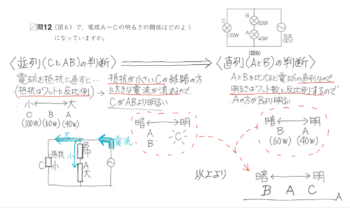
練習問題

 

複雑な回路の場合

直並列回路

 

 

並直列回路

 

オススメ教材

歴史の点数を上げたい受験生と保護者の方へ

年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試対策♪ 興味がある方はコチラへ